A matemática era a ciência pela qual Da Vinci buscava a constatação das coisas, e, para ele, não existia nenhuma evidência na natureza à qual não se pudesse aplicá-la. Já dizia o mestre: “Que nenhum homem que não seja matemático leia os elementos de minha obra“. Para Da Vinci, a demonstração matemática era o meio pelo qual se separava a mera especulação da verdadeira ciência: “Quem condena a suprema certeza da matemática alimenta-se da confusão e nunca poderá silenciar as contradições das ciências sofismáticas, que levam a um eterno charlatanismo“.

Para Leonardo, era essencial que o pintor tivesse conhecimentos de matemática para os estudos de perspectiva dos ambientes e proporções do corpo humano. Nos ateliês renascentistas, para além da arte, se estudavam matemática, física, anatomia e toda a espécie de ciências que aproximassem o objeto criado do seu criador e inspirador, a natureza. Aqui, aplica-se o princípio de Conessione, onde toda a parte (as ciências) tem a predisposição de unir-se ao todo (as ideias) para escapar a sua própria imperfeição (a forma). Pois como diz a máxima de Pitágoras, o limitado dá forma ao ilimitado. Todos as partes se conjugam para dar forma ao todo.

Na imagem 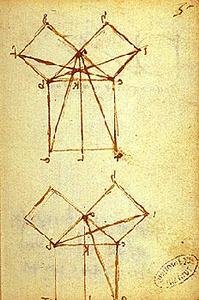ao lado¹, temos um estudo realizado por Da Vinci sobre o teorema de Pitágoras conforme a geometria Euclidiana. Para citar, Euclides é considerado como um dos grandes matemáticos da antiga Grécia, que escreveu diversas obras sobre a relação da geometria com a natureza das causas. Em um dos trechos de seu tratado de matemática, diz Da Vinci: “A geometria é infinita porque toda a quantidade contínua é divisível ao infinito em uma direção ou outra“, logo, a matemática dentro de sua concepção não possui limites no campo da imaginação.

Assim como Pitágoras, Da Vinci percebia a matemática como a fundação geométrica que dava origem à forma e ao movimento da vida: “…se começarmos com a superfície de um corpo, descobriremos que ela deriva de linhas, as fronteiras da superfície… sabemos que a linha, por sua vez é delimitada por pontos, e que o ponto é a última unidade, menor do que a qual nada existe“. Essa afirmação recorre à filosofia monista que defendia a origem comum de todas as coisas a partir de um elemento, neste caso, o ponto. Esse mesmo conceito já foi constatado pela nossa própria ciência ao chegar ao átomo, como elemento constituinte de toda a matéria.

Outro conceito interessante observado por Da Vinci, à sua época, era o da descontinuidade da matéria, pois hoje sabemos que 99,9% do espaço do átomo é vazio, logo, por mais que um corpo pareça compacto, a nível molecular, existem grandes espaços vazios entre cada uma das partículas. Ele exemplifica esta constatação na seguinte passagem de seu manuscrito sobre a fundação geométrica: “…muitos pontos imaginados em contato contínuo não constituem uma linha e, portanto, muitas linhas em contato contínuo ao longo das laterais não fazem uma superfície, nem muitas superfícies em contato contínuo fazem um corpo“.

Considerando a ideia da descontinuidade da matéria, Da Vinci questiona inclusive a fronteira que separa um elemento do outro, já que não há continuidade da matéria: “O contato do líquido com o sólido é uma superfície comum ao líquido e ao sólido. A superfície não forma parte de um nem de outro, é meramente a fronteira comum. Assim, a fronteira da água não forma parte nem da água nem do ar. Então o que divide o ar da água? Deve haver uma superfície que é a fronteira comum de dois corpos, e não forma parte de nenhum, pois se fizesse, teria um corpo divisível“.

Anaxágoras, filósofo contemporâneo de Pitágoras, também afirmava que a realidade pode ser reduzida a um número infinito de sementes, assim como a engenharia genética, que diz que uma cadeia de DNA possui todo o genoma humano. Conceitos como esse nos levam a um princípio comum, uma essência que está presente em tudo, da mesma forma como uma gota de água contém todo o oceano.

1 – Estudos de geometria euclidiana
Institut de France, Paris, Ms. K, 1503-07